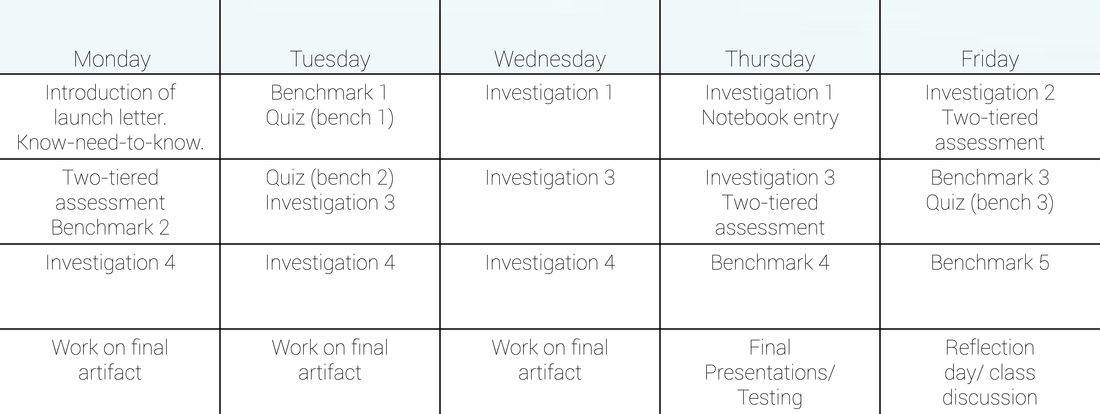
An essential element of Project-Based Instruction is that students engage in inquiry through a series of investigations. As mentioned in Bell et al. (2005), “The National Science Education Standards characterize inquiry instruction as involving students in a form of active learning that emphasizes questioning, data analysis, and critical thinking.” Various investigations have been developed for students to study Newton’s second law of motion, identify trigonometric ratios, and use these to calculate the magnitudes of different forces. In addition to the investigations, benchmark lessons were created to introduce necessary concepts for this project. As Trimarchi (2002) notes, “An interactive lesson is a method of conveying concepts, ideas, facts, and information that invites-and sometimes demands-active learning by students.” These lessons were developed in such a way that the students are actively engaged and are not just being fed facts and material. This not only benefits the students but also the teacher, as Trimarchi (2002) also indicates, “One of the benefits of interactive lecturing includes students giving immediate feedback to the teacher on an ongoing basis. This allows minute-by-minute adjustments as the lecture proceeds.”
Know Need to Know
In class notebooks the students should record a table with two columns. The left side is a list of information that the students know about the project from the launch letter. On the right side of the paper is the information that the students still need to know in order to complete the project.
Benchmark 1
Start the lesson by introducing the concept of forces to the students, "A force causes an object to change how it is moving." Allow a class discussion of how forces affect objects. Allow the students to answer in any way that they can, note that they have not yet developed a vocabulary for forces. Write some of the student answers on the board highlighting ones that describe static objects or objects in motion.
Have students demonstrate some of the given scenarios with objects around the room. For example, if one student says that forces make objects move have them demonstrate a force that moves an object. Discuss with the students what forces are acting upon that object. Allow them to bring up any ideas first to allow the students to own the concept. Make sure that gravity and reactive forces are brought up. What makes the object stop moving when the force is no longer applied? What makes the object not fall through the table if the only recognized force downward is gravity?
Give the students the challenge of analyzing forces on objects in given situations. They can represent their analysis in any way they want to, preferably with some type of drawing. This would be a great place to use a placemat method of assessment (Lin 36). Allow the students time to draw their own representation of the forces then collaborate with their groups before discussing as a class. Start to guide students to refine drawings down to the simplest representation of the forces. Guide students to represent magnitudes with different sized vectors. .
Students will be able to:
§112.39. Physics, Beginning with School Year 2010-2011 (One Credit).
(2) Scientific processes. The student uses a systematic approach to answer scientific laboratory and field
investigative questions. The student is expected to:
(K) communicate valid conclusions supported by the data through various methods such as lab reports,
labeled drawings, graphic organizers, journals, summaries, oral reports, and technology-based reports;
(4) Science concepts. The student knows and applies the laws governing motion in a variety of situations. The
student is expected to:
(D) calculate the effect of forces on objects, including the law of inertia, the relationship between force
and acceleration, and the nature of force pairs between objects;
(E) develop and interpret free-body force diagrams;
Investigation 1
Resource Lesson
Give students Newton’s 2nd Law of Motion before proceeding to the given lesson. In the lesson the students are working in groups to come up with an experiment which would verify that Newton’s 2nd Law of Motion works. They are to think of it as a hypothesis that needs to be confirmed. Give the students a selection of tools that are available in the classroom to perform their experiments. This can be as limited or free as your classroom allows, but the students should be given what list of supplies they have available to them prior to designing the experiment.
The groups should complete their plan for a lab and have teacher approval by day one and perform the experiment on day two. Remind the students that in conducting their experiment they may find that they do not come to a conclusion or the experiment may not work as they expected and that is okay. At the end of day two have the groups discuss what they could have done better in their experiment and have groups that did successfully recreate Newton’s 2nd Law explain what they did to the class.
Now that they have shown that if the object has a net force in one direction that it is accelerating. "What happens if the net force is zero? This is Newton's first law of motion. How do these laws of motion relate to our bridge design?"
The students should be given the opportunity to write notes from their experiment and the class discussion in a class notebook.
Students will be able to:
§112.39. Physics, Beginning with School Year 2010-2011 (One Credit).
(2) Scientific processes. The student uses a systematic approach to answer scientific laboratory and field investigative questions. The student is expected to:
(K) communicate valid conclusions supported by the data through various methods such as lab reports, labeled drawings, graphic organizers, journals, summaries, oral reports, and technology-based reports;
(4) Science concepts. The student knows and applies the laws governing motion in a variety of situations. The student is expected to:
(D) calculate the effect of forces on objects, including the law of inertia, the relationship between force and acceleration, and the nature of force pairs between objects;
(E) develop and interpret free-body force diagrams;
Investigation 2
Resource Lesson
Introduce the lesson by having students discuss triangles and where they have seen them used before. What does it mean for triangles to be similar? How is that different from congruence?
Each student should have a copy of the Discovering Trig worksheet. They may work in groups or alone measuring the lengths of the sides of each triangle as described on the worksheet. We suggest allowing them to only work on page one before gathering the class for a discussion. See if they noticed any patterns without seeing the calculator activity on the next page. “Would these ratios be the same for other triangles similar to these? What if the angle changed?”
After the class discussion the students can finish the last two pages which should confirm the patterns they may have discovered and allow them to write their thoughts on paper for teacher assessment.
Students will be able to:
§111.41. Geometry, Adopted 2012 (One Credit).
(1) Mathematical process standards. The student uses mathematical processes to acquire and demonstrate mathematical understanding. The student is expected to:
(A) apply mathematics to problems arising in everyday life, society, and the workplace;
(B) use a problem-solving model that incorporates analyzing given information, formulating a plan or strategy, determining a solution, justifying the solution, and evaluating the problem-solving process and the reasonableness of the solution;
(C) select tools, including real objects, manipulatives, paper and pencil, and technology as appropriate, and techniques, including mental math, estimation, and number sense as appropriate, to solve problems;
(D) communicate mathematical ideas, reasoning, and their implications using multiple representations, including symbols, diagrams, graphs, and language as appropriate;
(E) create and use representations to organize, record, and communicate mathematical ideas;
(F) analyze mathematical relationships to connect and communicate mathematical ideas; and
(G) display, explain, and justify mathematical ideas and arguments using precise mathematical language in written or oral communication.
(9) Similarity, proof, and trigonometry. The student uses the process skills to understand and apply relationships in right triangles. The student is expected to:
(A) determine the lengths of sides and measures of angles in a right triangle by applying the trigonometric ratios sine, cosine, and tangent to solve problems
§112.39. Physics, Beginning with School Year 2010-2011 (One Credit).
(2) Scientific processes. The student uses a systematic approach to answer scientific laboratory and field investigative questions. The student is expected to:
(K) communicate valid conclusions supported by the data through various methods such as lab reports, labeled drawings, graphic organizers, journals, summaries, oral reports, and technology-based reports;
(4) Science concepts. The student knows and applies the laws governing motion in a variety of situations. The student is expected to:
(D) calculate the effect of forces on objects, including the law of inertia, the relationship between force and acceleration, and the nature of force pairs between objects;
(E) develop and interpret free-body force diagrams;
Benchmark 2
The students will be arranged in groups. The class will be given a right triangle which includes a hypotenuse magnitude and one of the angles. Ask the students to solve for the legs of the triangle in their groups. This would be a great place to use the placemat method of assessment.
“What if this hypotenuse was a vector describing a force? How much is that force applied in the x direction only? What about the y direction only?”
Connect these x and y vectors to the term “vector components” so that the students know that vocabulary.
Give a second problem with just the x and y components and have the students discuss what that means for the net force. Connect the hypotenuse of the triangle to the term “resultant vector” so that the students know that vocabulary.
Lead a group discussion then a class discussion about why it may be useful to know the x and y vectors of a force separately from the net force. In what situations may you need to know that information?
Students will be able to:
§111.41. Geometry, Adopted 2012 (One Credit).
(9) Similarity, proof, and trigonometry. The student uses the process skills to understand and apply relationships in right triangles. The student is expected to:
(A) determine the lengths of sides and measures of angles in a right triangle by applying the trigonometric ratios sine, cosine, and tangent to solve problems
Investigation 3
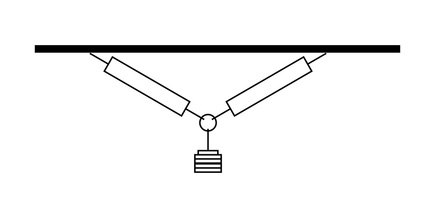
Each group of students will need to have 2 manual force gauges, 1 ring (like a key ring or similar), 1 hook for holding masses, a stand to hang the force gauges from, and 1 set of varying masses with known mass.
The initial setup should be one force gauge attached to the rod with a hook on the bottom to attach masses. Before adding any mass ask the students to predict what the force gauges will read in Newtons if you add 20 g of mass. Once the students have written down their predictions add the mass and have one student read the force gauge. "If I added 20 g to the force gauge why is it reading only 2 N?" Confirm here whether the students know the force = mass times acceleration. If not explain that the acceleration that the mass is experiencing is that of gravity.
The next setup should be as pictured below. Setup the force gauges and the ring in front of the class. Ask the students to predict what will happen to the two force gauges when you add mass to the ring.
In class notebooks the students should record a table with two columns. The left side is a list of information that the students know about the project from the launch letter. On the right side of the paper is the information that the students still need to know in order to complete the project.
Benchmark 1
Start the lesson by introducing the concept of forces to the students, "A force causes an object to change how it is moving." Allow a class discussion of how forces affect objects. Allow the students to answer in any way that they can, note that they have not yet developed a vocabulary for forces. Write some of the student answers on the board highlighting ones that describe static objects or objects in motion.
Have students demonstrate some of the given scenarios with objects around the room. For example, if one student says that forces make objects move have them demonstrate a force that moves an object. Discuss with the students what forces are acting upon that object. Allow them to bring up any ideas first to allow the students to own the concept. Make sure that gravity and reactive forces are brought up. What makes the object stop moving when the force is no longer applied? What makes the object not fall through the table if the only recognized force downward is gravity?
Give the students the challenge of analyzing forces on objects in given situations. They can represent their analysis in any way they want to, preferably with some type of drawing. This would be a great place to use a placemat method of assessment (Lin 36). Allow the students time to draw their own representation of the forces then collaborate with their groups before discussing as a class. Start to guide students to refine drawings down to the simplest representation of the forces. Guide students to represent magnitudes with different sized vectors. .
Students will be able to:
- draw a free body diagram to describe forces on an object.
- scale vectors on the free body diagram to represent the relative magnitudes of the forces.
- give a written explanation of the forces on an object given a free body diagram and explain a situation where the diagram is applicable.
§112.39. Physics, Beginning with School Year 2010-2011 (One Credit).
(2) Scientific processes. The student uses a systematic approach to answer scientific laboratory and field
investigative questions. The student is expected to:
(K) communicate valid conclusions supported by the data through various methods such as lab reports,
labeled drawings, graphic organizers, journals, summaries, oral reports, and technology-based reports;
(4) Science concepts. The student knows and applies the laws governing motion in a variety of situations. The
student is expected to:
(D) calculate the effect of forces on objects, including the law of inertia, the relationship between force
and acceleration, and the nature of force pairs between objects;
(E) develop and interpret free-body force diagrams;
Investigation 1
Resource Lesson
Give students Newton’s 2nd Law of Motion before proceeding to the given lesson. In the lesson the students are working in groups to come up with an experiment which would verify that Newton’s 2nd Law of Motion works. They are to think of it as a hypothesis that needs to be confirmed. Give the students a selection of tools that are available in the classroom to perform their experiments. This can be as limited or free as your classroom allows, but the students should be given what list of supplies they have available to them prior to designing the experiment.
The groups should complete their plan for a lab and have teacher approval by day one and perform the experiment on day two. Remind the students that in conducting their experiment they may find that they do not come to a conclusion or the experiment may not work as they expected and that is okay. At the end of day two have the groups discuss what they could have done better in their experiment and have groups that did successfully recreate Newton’s 2nd Law explain what they did to the class.
Now that they have shown that if the object has a net force in one direction that it is accelerating. "What happens if the net force is zero? This is Newton's first law of motion. How do these laws of motion relate to our bridge design?"
The students should be given the opportunity to write notes from their experiment and the class discussion in a class notebook.
Students will be able to:
- describe what it means for forces to be in equilibrium.
- use the sum of vectors in the x and y axes to determine if forces are in equilibrium.
§112.39. Physics, Beginning with School Year 2010-2011 (One Credit).
(2) Scientific processes. The student uses a systematic approach to answer scientific laboratory and field investigative questions. The student is expected to:
(K) communicate valid conclusions supported by the data through various methods such as lab reports, labeled drawings, graphic organizers, journals, summaries, oral reports, and technology-based reports;
(4) Science concepts. The student knows and applies the laws governing motion in a variety of situations. The student is expected to:
(D) calculate the effect of forces on objects, including the law of inertia, the relationship between force and acceleration, and the nature of force pairs between objects;
(E) develop and interpret free-body force diagrams;
Investigation 2
Resource Lesson
Introduce the lesson by having students discuss triangles and where they have seen them used before. What does it mean for triangles to be similar? How is that different from congruence?
Each student should have a copy of the Discovering Trig worksheet. They may work in groups or alone measuring the lengths of the sides of each triangle as described on the worksheet. We suggest allowing them to only work on page one before gathering the class for a discussion. See if they noticed any patterns without seeing the calculator activity on the next page. “Would these ratios be the same for other triangles similar to these? What if the angle changed?”
After the class discussion the students can finish the last two pages which should confirm the patterns they may have discovered and allow them to write their thoughts on paper for teacher assessment.
Students will be able to:
- describe the relationship between an identified angle of a right triangle and the sides of the same triangle and similar triangles.
- use trigonometric ratios to calculate the measure of the sides and angles of right triangles.
§111.41. Geometry, Adopted 2012 (One Credit).
(1) Mathematical process standards. The student uses mathematical processes to acquire and demonstrate mathematical understanding. The student is expected to:
(A) apply mathematics to problems arising in everyday life, society, and the workplace;
(B) use a problem-solving model that incorporates analyzing given information, formulating a plan or strategy, determining a solution, justifying the solution, and evaluating the problem-solving process and the reasonableness of the solution;
(C) select tools, including real objects, manipulatives, paper and pencil, and technology as appropriate, and techniques, including mental math, estimation, and number sense as appropriate, to solve problems;
(D) communicate mathematical ideas, reasoning, and their implications using multiple representations, including symbols, diagrams, graphs, and language as appropriate;
(E) create and use representations to organize, record, and communicate mathematical ideas;
(F) analyze mathematical relationships to connect and communicate mathematical ideas; and
(G) display, explain, and justify mathematical ideas and arguments using precise mathematical language in written or oral communication.
(9) Similarity, proof, and trigonometry. The student uses the process skills to understand and apply relationships in right triangles. The student is expected to:
(A) determine the lengths of sides and measures of angles in a right triangle by applying the trigonometric ratios sine, cosine, and tangent to solve problems
§112.39. Physics, Beginning with School Year 2010-2011 (One Credit).
(2) Scientific processes. The student uses a systematic approach to answer scientific laboratory and field investigative questions. The student is expected to:
(K) communicate valid conclusions supported by the data through various methods such as lab reports, labeled drawings, graphic organizers, journals, summaries, oral reports, and technology-based reports;
(4) Science concepts. The student knows and applies the laws governing motion in a variety of situations. The student is expected to:
(D) calculate the effect of forces on objects, including the law of inertia, the relationship between force and acceleration, and the nature of force pairs between objects;
(E) develop and interpret free-body force diagrams;
Benchmark 2
The students will be arranged in groups. The class will be given a right triangle which includes a hypotenuse magnitude and one of the angles. Ask the students to solve for the legs of the triangle in their groups. This would be a great place to use the placemat method of assessment.
“What if this hypotenuse was a vector describing a force? How much is that force applied in the x direction only? What about the y direction only?”
Connect these x and y vectors to the term “vector components” so that the students know that vocabulary.
Give a second problem with just the x and y components and have the students discuss what that means for the net force. Connect the hypotenuse of the triangle to the term “resultant vector” so that the students know that vocabulary.
Lead a group discussion then a class discussion about why it may be useful to know the x and y vectors of a force separately from the net force. In what situations may you need to know that information?
Students will be able to:
- describe how vector components are related to vector addition
- draw a vector's x and y components and solve for their magnitudes using trigonometric ratios
§111.41. Geometry, Adopted 2012 (One Credit).
(9) Similarity, proof, and trigonometry. The student uses the process skills to understand and apply relationships in right triangles. The student is expected to:
(A) determine the lengths of sides and measures of angles in a right triangle by applying the trigonometric ratios sine, cosine, and tangent to solve problems
Investigation 3
Each group of students will need to have 2 manual force gauges, 1 ring (like a key ring or similar), 1 hook for holding masses, a stand to hang the force gauges from, and 1 set of varying masses with known mass.
The initial setup should be one force gauge attached to the rod with a hook on the bottom to attach masses. Before adding any mass ask the students to predict what the force gauges will read in Newtons if you add 20 g of mass. Once the students have written down their predictions add the mass and have one student read the force gauge. "If I added 20 g to the force gauge why is it reading only 2 N?" Confirm here whether the students know the force = mass times acceleration. If not explain that the acceleration that the mass is experiencing is that of gravity.
The next setup should be as pictured below. Setup the force gauges and the ring in front of the class. Ask the students to predict what will happen to the two force gauges when you add mass to the ring.
Once the students have written predictions down or expressed them out loud place the masses on the hook and let the force gauges settle. Have a student note what the reading is on each of the force gauges. “If the mass we applied was ___ why did the force gauges read ___?” "Is this what you predicted? Why is this different from the last example?"
Ask students to draw free body diagrams for the ring with all of the forces acting on the ring represented by vectors. This would be a great place to use a placemat method of assessment (Lin 36). At this point in the project the students should know how to draw vector components and can use their knowledge of trigonometric functions to solve for the magnitudes of the forces acting on the force gauges. Have a group present their explanation.
During the next class period students should have the opportunity to ask their own question. They should be allowed to set up the force gauges and masses in any configuration that is safe. They will have to explain their question and findings using free body diagrams. Encourage them to explore different angles for force application. Allow the students time to write up explanations for their findings and other questions they may have for the teacher to evaluate.
Students will be able to:
Benchmark 3
Now that we have looked at how forces act on a single object using free body diagrams, we are going to look at how an applied force acts on a structure. The students will be investigating both a triangle and a square structure to compare the carrying capacity of both.
Each student should have a worksheet for this benchmark. It will guide them by giving them the shapes they will be analyzing.
On the worksheets the students should be able to draw a free body diagram for each point where members of the structure connects.
From there they use their knowledge about equilibrium forces to write equations for each free body diagram. They can then begin to solve for the missing force values. The students should conclude that the triangle can support more weight because the members are supporting less force per member. Ask the students: “Do you think that a combination of shapes is stronger than an individual shape?” They will need to consider this for the next step, designing their bridge.
Students will be able to:
§111.41. Geometry, Adopted 2012 (One Credit).
(1) Mathematical process standards. The student uses mathematical processes to acquire and demonstrate mathematical understanding. The student is expected to:
(A) apply mathematics to problems arising in everyday life, society, and the workplace;
(B) use a problem-solving model that incorporates analyzing given information, formulating a plan or strategy, determining a solution, justifying the solution, and evaluating the problem-solving process and the reasonableness of the solution;
(C) select tools, including real objects, manipulatives, paper and pencil, and technology as appropriate, and techniques, including mental math, estimation, and number sense as appropriate, to solve problems;
(D) communicate mathematical ideas, reasoning, and their implications using multiple representations, including symbols, diagrams, graphs, and language as appropriate;
(E) create and use representations to organize, record, and communicate mathematical ideas;
(F) analyze mathematical relationships to connect and communicate mathematical ideas; and
(G) display, explain, and justify mathematical ideas and arguments using precise mathematical language in written or oral communication.
(9) Similarity, proof, and trigonometry. The student uses the process skills to understand and apply relationships in right triangles. The student is expected to:
(A) determine the lengths of sides and measures of angles in a right triangle by applying the trigonometric ratios sine, cosine, and tangent to solve problems
§112.39. Physics, Beginning with School Year 2010-2011 (One Credit).
(2) Scientific processes. The student uses a systematic approach to answer scientific laboratory and field investigative questions. The student is expected to:
(K) communicate valid conclusions supported by the data through various methods such as lab reports, labeled drawings, graphic organizers, journals, summaries, oral reports, and technology-based reports;
(4) Science concepts. The student knows and applies the laws governing motion in a variety of situations. The student is expected to:
(D) calculate the effect of forces on objects, including the law of inertia, the relationship between force and acceleration, and the nature of force pairs between objects;
(E) develop and interpret free-body force diagrams
Investigation 4
The students will begin designing their bridge within their groups. Prompt the students to sketch designs and ideas in their class notebooks so they can refer to them later. Remind the students what their driving question is, "What is your goal for your bridge? What is necessary to have a winning design?" It may be necessary to have students return to the know need to know page of the class notebook to rethink about what the design goal is and review what they have learned so far. At this time if they have any final questions they can ask them. The students will spend the first day brainstorming configurations of shapes into bridge structures.
The second day of the investigation the teacher can encourage students to think about how angles affect the amount of force a member supports. "How does the force on each member change when the angle of the joint is changed?"
Students will be able to:
Benchmark 4
Students will have the opportunity to critique each other’s work using the same rubric that the teacher will use to evaluate the final artifact. Each group of students will be handed copies of the final artifact rubric. They will swap bridge designs with another group and evaluate the design based on the rubric. They should also take some time to check the mathematics used in the design. Think: is the design sturdy? will it hold the mass the group claims the bridge will hold?
Students will be able to:
Benchmark 5
Start the class by addressing that at the end of this week the students' final artifacts will be due. At this point they have all investigated how to design a bridge and calculate how much mass it can support. They have had the opportunity to critique each other's designs and modify their own. They should be ready to build their final models. Inform the class that after the model demonstrations there will be a writing assignment in which they are to address successes and failures in their design and how the model could have been improved. They will also need to address any discrepancy between their predicted carrying capacity and the actual carrying capacity.
With this information, the class will come up with a list of measurements that they want to take when they test their models. They should take into consideration what equipment is available for taking measurements and what measurements can realistically be taken when the model is broken. What are the most important pieces of information they will need to write about potential failures and room for improvement?
Students will be able to:
§112.39. Physics, Beginning with School Year 2010-2011 (One Credit).
(2) Scientific processes. The student uses a systematic approach to answer scientific laboratory and field investigative questions. The student is expected to:
(E) design and implement investigative procedures, including making observations, asking well-defined questions, formulating testable hypotheses, identifying variables, selecting appropriate equipment and technology, and evaluating numerical answers for reasonableness;
§130.362. Concepts of Engineering and Technology (One-Half to One Credit).
(6) The student thinks critically and applies fundamental principles of system modeling and design to multiple design projects. The student is expected to:
(A) identify and describe the fundamental processes needed for a project, including design and prototype development;
(C) use problem-solving techniques to develop technological solutions;
(D) use consistent units for all measurements and computations
Ask students to draw free body diagrams for the ring with all of the forces acting on the ring represented by vectors. This would be a great place to use a placemat method of assessment (Lin 36). At this point in the project the students should know how to draw vector components and can use their knowledge of trigonometric functions to solve for the magnitudes of the forces acting on the force gauges. Have a group present their explanation.
During the next class period students should have the opportunity to ask their own question. They should be allowed to set up the force gauges and masses in any configuration that is safe. They will have to explain their question and findings using free body diagrams. Encourage them to explore different angles for force application. Allow the students time to write up explanations for their findings and other questions they may have for the teacher to evaluate.
Students will be able to:
- use an electronic or manual force gauge to measure force on an object.
- draw free body diagrams representing forces acting on an object.
- account for magnitude of forces when drawing free body diagrams.
- draw a vector's x and y components and solve for their magnitudes using trigonometric ratios
- use the sum of vectors in the x and y axes to determine if forces are in equilibrium.
Benchmark 3
Now that we have looked at how forces act on a single object using free body diagrams, we are going to look at how an applied force acts on a structure. The students will be investigating both a triangle and a square structure to compare the carrying capacity of both.
Each student should have a worksheet for this benchmark. It will guide them by giving them the shapes they will be analyzing.
On the worksheets the students should be able to draw a free body diagram for each point where members of the structure connects.
From there they use their knowledge about equilibrium forces to write equations for each free body diagram. They can then begin to solve for the missing force values. The students should conclude that the triangle can support more weight because the members are supporting less force per member. Ask the students: “Do you think that a combination of shapes is stronger than an individual shape?” They will need to consider this for the next step, designing their bridge.
Students will be able to:
- use free body diagrams to show how applied forces will distribute through a structure.
- use knowledge of sum of vectors in equilibrium and systems of equations to solve for the magnitude of forces on members of the structure.
§111.41. Geometry, Adopted 2012 (One Credit).
(1) Mathematical process standards. The student uses mathematical processes to acquire and demonstrate mathematical understanding. The student is expected to:
(A) apply mathematics to problems arising in everyday life, society, and the workplace;
(B) use a problem-solving model that incorporates analyzing given information, formulating a plan or strategy, determining a solution, justifying the solution, and evaluating the problem-solving process and the reasonableness of the solution;
(C) select tools, including real objects, manipulatives, paper and pencil, and technology as appropriate, and techniques, including mental math, estimation, and number sense as appropriate, to solve problems;
(D) communicate mathematical ideas, reasoning, and their implications using multiple representations, including symbols, diagrams, graphs, and language as appropriate;
(E) create and use representations to organize, record, and communicate mathematical ideas;
(F) analyze mathematical relationships to connect and communicate mathematical ideas; and
(G) display, explain, and justify mathematical ideas and arguments using precise mathematical language in written or oral communication.
(9) Similarity, proof, and trigonometry. The student uses the process skills to understand and apply relationships in right triangles. The student is expected to:
(A) determine the lengths of sides and measures of angles in a right triangle by applying the trigonometric ratios sine, cosine, and tangent to solve problems
§112.39. Physics, Beginning with School Year 2010-2011 (One Credit).
(2) Scientific processes. The student uses a systematic approach to answer scientific laboratory and field investigative questions. The student is expected to:
(K) communicate valid conclusions supported by the data through various methods such as lab reports, labeled drawings, graphic organizers, journals, summaries, oral reports, and technology-based reports;
(4) Science concepts. The student knows and applies the laws governing motion in a variety of situations. The student is expected to:
(D) calculate the effect of forces on objects, including the law of inertia, the relationship between force and acceleration, and the nature of force pairs between objects;
(E) develop and interpret free-body force diagrams
Investigation 4
The students will begin designing their bridge within their groups. Prompt the students to sketch designs and ideas in their class notebooks so they can refer to them later. Remind the students what their driving question is, "What is your goal for your bridge? What is necessary to have a winning design?" It may be necessary to have students return to the know need to know page of the class notebook to rethink about what the design goal is and review what they have learned so far. At this time if they have any final questions they can ask them. The students will spend the first day brainstorming configurations of shapes into bridge structures.
The second day of the investigation the teacher can encourage students to think about how angles affect the amount of force a member supports. "How does the force on each member change when the angle of the joint is changed?"
Students will be able to:
- use knowledge of forces to assess their bridge design and maximize its ability to support mass.
- make changes to designs based on reasoning
Benchmark 4
Students will have the opportunity to critique each other’s work using the same rubric that the teacher will use to evaluate the final artifact. Each group of students will be handed copies of the final artifact rubric. They will swap bridge designs with another group and evaluate the design based on the rubric. They should also take some time to check the mathematics used in the design. Think: is the design sturdy? will it hold the mass the group claims the bridge will hold?
Students will be able to:
- use a rubric to critique and revise bridge designs.
- communicate mathematical findings effectively.
Benchmark 5
Start the class by addressing that at the end of this week the students' final artifacts will be due. At this point they have all investigated how to design a bridge and calculate how much mass it can support. They have had the opportunity to critique each other's designs and modify their own. They should be ready to build their final models. Inform the class that after the model demonstrations there will be a writing assignment in which they are to address successes and failures in their design and how the model could have been improved. They will also need to address any discrepancy between their predicted carrying capacity and the actual carrying capacity.
With this information, the class will come up with a list of measurements that they want to take when they test their models. They should take into consideration what equipment is available for taking measurements and what measurements can realistically be taken when the model is broken. What are the most important pieces of information they will need to write about potential failures and room for improvement?
Students will be able to:
- Identify which measurements and data values would be most useful to compare chosen aspects of the bridge.
- Collect measurements from bridge model and experiment.
- Develop a procedure to test their model including most appropriate tools and equipment for collecting the data.
§112.39. Physics, Beginning with School Year 2010-2011 (One Credit).
(2) Scientific processes. The student uses a systematic approach to answer scientific laboratory and field investigative questions. The student is expected to:
(E) design and implement investigative procedures, including making observations, asking well-defined questions, formulating testable hypotheses, identifying variables, selecting appropriate equipment and technology, and evaluating numerical answers for reasonableness;
§130.362. Concepts of Engineering and Technology (One-Half to One Credit).
(6) The student thinks critically and applies fundamental principles of system modeling and design to multiple design projects. The student is expected to:
(A) identify and describe the fundamental processes needed for a project, including design and prototype development;
(C) use problem-solving techniques to develop technological solutions;
(D) use consistent units for all measurements and computations